Second Intro to GA

This post has been taken from http://www.obitko.com/tutorials/genetic-algorithms

Genetic algorithms are a part of evolutionary computing, which is a rapidly growing area of artificial intelligence.

As you can guess, genetic algorithms are inspired by Darwin's theory about evolution. Simply said, solution to a problem solved by genetic algorithms is evolved.

---

History

Idea of evolutionary computing was introduced in the 1960s by I. Rechenberg in his work "Evolution strategies" (Evolutionsstrategie in original). His idea was then developed by other researchers. Genetic Algorithms (GAs) were invented by John Holland and developed by him and his students and colleagues. This lead to Holland's book "Adaption in Natural and Artificial Systems" published in 1975.

In 1992 John Koza has used genetic algorithm to evolve programs to perform certain tasks. He called his method "genetic programming" (GP). LISP programs were used, because programs in this language can expressed in the form of a "parse tree", which is the object the GA works on.

All living organisms consist of cells. In each cell there is the same set of chromosomes. Chromosomes are strings of DNA and serves as a model for the whole organism. A chromosome consist of genes, blocks of DNA. Each gene encodes a particular protein. Basically can be said, that each gene encodes a trait, for example color of eyes. Possible settings for a trait (e.g. blue, brown) are called alleles. Each gene has its own position in the chromosome. This position is called locus.

Complete set of genetic material (all chromosomes) is called genome. Particular set of genes in genome is called genotype. The genotype is with later development after birth base for the organism's phenotype, its physical and mental characteristics, such as eye color, intelligence etc.

Reproduction

During reproduction, first occurs recombination (or crossover). Genes from parents form in some way the whole new chromosome. The new created offspring can then be mutated. Mutation means, that the elements of DNA are a bit changed. This changes are mainly caused by errors in copying genes from parents.

The fitness of an organism is measured by success of the organism in its life.

If we are solving some problem, we are usually looking for some solution, which will be the best among others. The space of all feasible solutions (it means objects among those the desired solution is) is called search space (also state space). Each point in the search space represent one feasible solution. Each feasible solution can be "marked" by its value or fitness for the problem. We are looking for our solution, which is one point (or more) among feasible solutions - that is one point in the search space.

The looking for a solution is then equal to a looking for some extreme (minimum or maximum) in the search space. The search space can be whole known by the time of solving a problem, but usually we know only a few points from it and we are generating other points as the process of finding solution continues.

The problem is that the search can be very complicated. One does not know where to look for the solution and where to start. There are many methods, how to find some suitable solution (ie. not necessarily the best solution), for example hill climbing, tabu search, simulated annealing and genetic algorithm. The solution found by this methods is often considered as a good solution, because it is not often possible to prove what is the real optimum.

NP-hard Problems

Example of difficult problems, which cannot be solved int "traditional" way, are NP problems.

There are many tasks for which we know fast (polynomial) algorithms. There are also some problems that are not possible to be solved algorithmicaly. For some problems was proved that they are not solvable in polynomial time.

But there are many important tasks, for which it is very difficult to find a solution, but once we have it, it is easy to check the solution. This fact led to NP-complete problems. NP stands for nondeterministic polynomial and it means that it is possible to "guess" the solution (by some nondeterministic algorithm) and then check it, both in polynomial time. If we had a machine that can guess, we would be able to find a solution in some reasonable time.

Studying of NP-complete problems is for simplicity restricted to the problems, where the answer can be yes or no. Because there are tasks with complicated outputs, a class of problems called NP-hard problems has been introduced. This class is not as limited as class of NP-complete problems.

For NP-problems is characteristic that some simple algorithm to find a solution is obvious at a first sight - just trying all possible solutions. But this algorithm is very slow (usually O(2^n)) and even for a bit bigger instances of the problems it is not usable at all.

Today nobody knows if some faster exact algorithm exists. Proving or disproving this remains as a big task for new researchers (and maybe you! :-)). Today many people think, that such an algorithm does not exist and so they are looking for some alternative methods - example of these methods are genetic algorithms.

Outline of the Basic Genetic Algorithm

1. [Start] Generate random population of n chromosomes (suitable solutions for the problem)
2. [Fitness] Evaluate the fitness f(x) of each chromosome x in the population
3. [New population] Create a new population by repeating following steps until the new population is complete
   1. [Selection] Select two parent chromosomes from a population according to their fitness (the better fitness, the bigger chance to be selected)
   2. [Crossover] With a crossover probability cross over the parents to form a new offspring (children). If no crossover was performed, offspring is an exact copy of parents.
   3. [Mutation] With a mutation probability mutate new offspring at each locus (position in chromosome).
   4. [Accepting] Place new offspring in a new population
4. [Replace] Use new generated population for a further run of algorithm
5. [Test] If the end condition is satisfied, stop, and return the best solution in current population
6. [Loop] Go to step 2

Some Comments

As you can see, the outline of Basic GA is very general. There are many things that can be implemented differently in various problems.

First question is how to create chromosomes, what type of encoding choose. With this is connected crossover and mutation, the two basic operators of GA. Encoding, crossover and mutation are introduced in next chapter.

Next questions is how to select parents for crossover. This can be done in many ways, but the main idea is to select the better parents (in hope that the better parents will produce better offspring). Also you may think, that making new population only by new offspring can cause lost of the best chromosome from the last population. This is true, so so called elitism is often used. This means, that at least one best solution is copied without changes to a new population, so the best solution found can survive to end of run.

Operators of GA

Encoding of a Chromosome

The chromosome should in some way contain information about solution which it represents. The most used way of encoding is a binary string. The chromosome then could look like this:

Chromosome 1	1101100100110110
Chromosome 2	1101111000011110

Each chromosome has one binary string. Each bit in this string can represent some characteristic of the solution. Or the whole string can represent a number .

Of course, there are many other ways of encoding. This depends mainly on the solved problem. For example, one can encode directly integer or real numbers, sometimes it is useful to encode some permutations and so on.

Crossover

After we have decided what encoding we will use, we can make a step to crossover. Crossover selects genes from parent chromosomes and creates a new offspring. The simplest way how to do this is to choose randomly some crossover point and everything before this point point copy from a first parent and then everything after a crossover point copy from the second parent.

Crossover can then look like this ( | is the crossover point):

Chromosome 1	11011 | 00100110110
Chromosome 2	11011 | 11000011110
Offspring 1	11011 | 11000011110
Offspring 2	11011 | 00100110110

There are other ways how to make crossover, for example we can choose more crossover points. Crossover can be rather complicated and very depends on encoding of the encoding of chromosome. Specific crossover made for a specific problem can improve performance of the genetic algorithm.

Mutation

After a crossover is performed, mutation take place. This is to prevent falling all solutions in population into a local optimum of solved problem. Mutation changes randomly the new offspring. For binary encoding we can switch a few randomly chosen bits from 1 to 0 or from 0 to 1. Mutation can then be following:

Original offspring 1	1101111000011110
Original offspring 2	1101100100110110
Mutated offspring 1	1100111000011110
Mutated offspring 2	1101101100110110

The mutation depends on the encoding as well as the crossover. For example when we are encoding permutations, mutation could be exchanging two genes.

Parameters of GA

There are two basic parameters of GA - crossover probability and mutation probability. Crossover probability says how often will be crossover performed. If there is no crossover, offspring is exact copy of parents. If there is a crossover, offspring is made from parts of parents' chromosome. If crossover probability is 100%, then all offspring is made by crossover. If it is 0%, whole new generation is made from exact copies of chromosomes from old population (but this does not mean that the new generation is the same!)

rossover is made in hope that new chromosomes will have good parts of old chromosomes and maybe the new chromosomes will be better. However it is good to leave some part of population survive to next generation.

Mutation probability says how often will be parts of chromosome mutated. If there is no mutation, offspring is taken after crossover (or copy) without any change. If mutation is performed, part of chromosome is changed. If mutation probability is 100%, whole chromosome is changed, if it is 0%, nothing is changed.
Mutation is made to prevent falling GA into local extreme, but it should not occur very often, because then GA will in fact change to random search.

Other Parameters

There are also some other parameters of GA. One also important parameter is population size.

Population size says how many chromosomes are in population (in one generation). If there are too few chromosomes, GA have a few possibilities to perform crossover and only a small part of search space is explored. On the other hand, if there are too many chromosomes, GA slows down. Research shows that after some limit (which depends mainly on encoding and the problem) it is not useful to increase population size, because it does not make solving the problem faster.

Selection

chromosomes are selected from the population to be parents to crossover. The problem is how to select these chromosomes. According to Darwin's evolution theory the best ones should survive and create new offspring. There are many methods how to select the best chromosomes, for example roulette wheel selection, Boltzman selection, tournament selection, rank selection, steady state selection and some others.

Roulette Wheel Selection

Parents are selected according to their fitness. The better the chromosomes are, the more chances to be selected they have. Imagine a roulette wheel where are placed all chromosomes in the population, every has its place big accordingly to its fitness function, like on the following picture.

Then a marble is thrown there and selects the chromosome. Chromosome with bigger fitness will be selected more times.

This can be simulated by following algorithm.

1. [Sum] Calculate sum of all chromosome fitnesses in population - sum S.
2. [Select] Generate random number from interval (0,S) - r.
3. [Loop] Go through the population and sum fitnesses from 0 - sum s. When the sum s is greater then r, stop and return the chromosome where you are.

Of course, step 1 is performed only once for each population.

Rank Selection

The previous selection will have problems when the fitnesses differs very much. For example, if the best chromosome fitness is 90% of all the roulette wheel then the other chromosomes will have very few chances to be selected.

Rank selection first ranks the population and then every chromosome receives fitness from this ranking. The worst will have fitness 1, second worst 2 etc. and the best will have fitness N (number of chromosomes in population).

You can see in following picture, how the situation changes after changing fitness to order number.

Situation before ranking (graph of fitnesses)

Situation after ranking (graph of order numbers)

After this all the chromosomes have a chance to be selected. But this method can lead to slower convergence, because the best chromosomes do not differ so much from other ones.

Steady-State Selection

This is not particular method of selecting parents. Main idea of this selection is that big part of chromosomes should survive to next generation.

GA then works in a following way. In every generation are selected a few (good - with high fitness) chromosomes for creating a new offspring. Then some (bad - with low fitness) chromosomes are removed and the new offspring is placed in their place. The rest of population survives to new generation.

Elitism

Idea of elitism has been already introduced. When creating new population by crossover and mutation, we have a big chance, that we will loose the best chromosome.

Elitism is name of method, which first copies the best chromosome (or a few best chromosomes) to new population. The rest is done in classical way. Elitism can very rapidly increase performance of GA, because it prevents losing the best found solution.

Encoding

Binary Encoding

Binary encoding is the most common, mainly because first works about GA used this type of encoding.

In binary encoding every chromosome is a string of bits, 0 or 1.

Chromosome A	101100101100101011100101
Chromosome B	111111100000110000011111

Example of chromosomes with binary encoding

Binary encoding gives many possible chromosomes even with a small number of alleles. On the other hand, this encoding is often not natural for many problems and sometimes corrections must be made after crossover and/or mutation.

Permutation Encoding

Permutation encoding can be used in ordering problems, such as travelling salesman problem or task ordering problem.

In permutation encoding, every chromosome is a string of numbers, which represents number in a sequence.

Chromosome A	1 5 3 2 6 4 7 9 8
Chromosome B	8 5 6 7 2 3 1 4 9

Example of chromosomes with permutation encoding

Permutation encoding is only useful for ordering problems. Even for this problems for some types of crossover and mutation corrections must be made to leave the chromosome consistent (i.e. have real sequence in it).

Value Encoding

Direct value encoding can be used in problems, where some complicated value, such as real numbers, are used. Use of binary encoding for this type of problems would be very difficult.

In value encoding, every chromosome is a string of some values. Values can be anything connected to problem, form numbers, real numbers or chars to some complicated objects.

Chromosome A	1.2324 5.3243 0.4556 2.3293 2.4545
Chromosome B	ABDJEIFJDHDIERJFDLDFLFEGT
Chromosome C	(back), (back), (right), (forward), (left)

Example of chromosomes with value encoding

Value encoding is very good for some special problems. On the other hand, for this encoding is often necessary to develop some new crossover and mutation specific for the problem.

Tree Encoding

Tree encoding is used mainly for evolving programs or expressions, for genetic programming.

In tree encoding every chromosome is a tree of some objects, such as functions or commands in programming language.

Chromosome A	Chromosome B
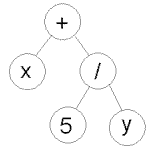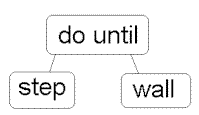( + x ( / 5 y ) )	( do_until step wall )

Example of chromosomes with tree encoding

Tree encoding is good for evolving programs. Programing language LISP is often used to this, because programs in it are represented in this form and can be easily parsed as a tree, so the crossover and mutation can be done relatively easily.

Crossover and Mutation

Binary Encoding

Crossover

Single point crossover - one crossover point is selected, binary string from beginning of chromosome to the crossover point is copied from one parent, the rest is copied from the second parent

11001011+11011111 = 11001111

Two point crossover - two crossover point are selected, binary string from beginning of chromosome to the first crossover point is copied from one parent, the part from the first to the second crossover point is copied from the second parent and the rest is copied from the first parent

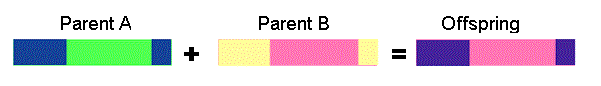
11001011 + 11011111 = 11011111

Uniform crossover - bits are randomly copied from the first or from the second parent

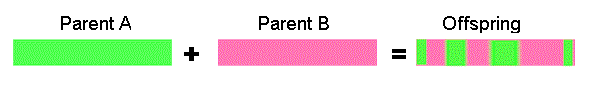
11001011 + 11011101 = 11011111

Arithmetic crossover - some arithmetic operation is performed to make a new offspring

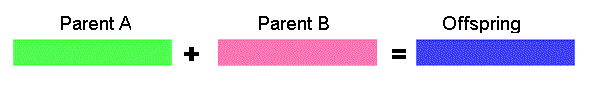
11001011 + 11011111 = 11001001 (AND)

Mutation

Bit inversion - selected bits are inverted

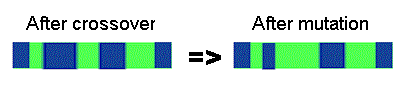
11001001 => 10001001

Permutation Encoding

Crossover

Single point crossover - one crossover point is selected, till this point the permutation is copied from the first parent, then the second parent is scanned and if the number is not yet in the offspring it is added
Note: there are more ways how to produce the rest after crossover point

(1 2 3 4 5 6 7 8 9) + (4 5 3 6 8 9 7 2 1) = (1 2 3 4 5 6 8 9 7)

Mutation

Order changing - two numbers are selected and exchanged

(1 2 3 4 5 6 8 9 7) => (1 8 3 4 5 6 2 9 7)

Value Encoding

Crossover

All crossovers from binary encoding can be used

Mutation

Adding a small number (for real value encoding) - to selected values is added (or subtracted) a small number

(1.29 5.68 2.86 4.11 5.55) => (1.29 5.68 2.73 4.22 5.55)

Tree Encoding

Crossover

Tree crossover - in both parent one crossover point is selected, parents are divided in that point and exchange part below crossover point to produce new offspring

Mutation

Changing operator, number - selected nodes are changed

Recommendations

Recommendations are often results of some empiric studies of GAs, which were often performed only on binary encoding.

• Crossover rate
  Crossover rate generally should be high, about 80%-95%. (However some results show that for some problems crossover rate about 60% is the best.)
• Mutation rate
  On the other side, mutation rate should be very low. Best rates reported are about 0.5%-1%.
• Population size
  It may be surprising, that very big population size usually does not improve performance of GA (in meaning of speed of finding solution). Good population size is about 20-30, however sometimes sizes 50-100 are reported as best. Some research also shows, that best population size depends on encoding, on size of encoded string. It means, if you have chromosome with 32 bits, the population should be say 32, but surely two times more than the best population size for chromosome with 16 bits.
• Selection
  Basic roulette wheel selection can be used, but sometimes rank selection can be better. Check chapter about selection for advantages and disadvantages. There are also some more sophisticated method, which changes parameters of selection during run of GA. Basically they behaves like simulated annealing. But surely elitism should be used (if you do not use other method for saving the best found solution). You can also try steady state selection.
• Encoding
  Encoding depends on the problem and also on the size of instance of the problem.
  
• Crossover and mutation type
  Operators depend on encoding and on the problem

  Applications of GA

  Genetic algorithms has been used for difficult problems (such as NP-hard problems), for machine learning and also for evolving simple programs. They have been also used for some art, for evolving pictures and music.

  Advantage of GAs is in their parallelism. GA is travelling in a search space with more individuals (and with genotype rather than phenotype) so they are less likely to get stuck in a local extreme like some other methods.

  They are also easy to implement. Once you have some GA, you just have to write new chromosome (just one object) to solve another problem. With the same encoding you just change the fitness function and it is all.On the other hand, choosing encoding and fitness function can be difficult.

  Disadvantage of GAs is in their computational time. They can be slower than some other methods. But with todays computers it is not so big problem.

  To get an idea about problems solved by GA, here is a short list of some applications:
  

• Nonlinear dynamical systems - predicting, data analysis
• Designing neural networks, both architecture and weights
• Robot trajectory
• Evolving LISP programs (genetic programming)
• Strategy planning
• Finding shape of protein molecules
• TSP and sequence scheduling
• Functions for creating images