Important Disclaimer

The purpose of this blog is purely to serve as a compilation of good technical material for my students. No financial or other motives are involved. Most of the content in this blog has been reproduced from other sources. I have made every attempt to mention the source link at the beginning of each blog. All readers are requested to kindly acknowledge that source and not this blog, in case you find the post helpful. However, I have not been able to trace the source links for some of my older posts. I wish to emphasize that this is not intentional and any help in this regard would be appreciated.

Jul 23, 2011

Polynomial Fitting- Least Squares

This post has been taken from: Weisstein, Eric W. "Least Squares Fitting--Polynomial." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html

Kindly acknowledge the above source and not this blog. The material has been presented here to serve as learning material for my students. No commercial activity is involved.

Generalizing from a straight line (i.e., first degree polynomial) to a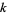 kth degree polynomial
y=a_0+a_1x+...+a_kx^k,
(1)
the residual is given by
R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2.
(2)
The partial derivatives (again dropping superscripts) are
(partial(R^2))/(partiala_0)=-2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]=0
(3)
(partial(R^2))/(partiala_1)=-2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x=0
(4)
(partial(R^2))/(partiala_k)=-2sum_(i=1)^(n)[y-(a_0+a_1x+...+a_kx^k)]x^k=0.
(5)
These lead to the equations
a_0n+a_1sum_(i=1)^(n)x_i+...+a_ksum_(i=1)^(n)x_i^k=sum_(i=1)^(n)y_i
(6)
a_0sum_(i=1)^(n)x_i+a_1sum_(i=1)^(n)x_i^2+...+a_ksum_(i=1)^(n)x_i^(k+1)=sum_(i=1)^(n)x_iy_i
(7)
a_0sum_(i=1)^(n)x_i^k+a_1sum_(i=1)^(n)x_i^(k+1)+...+a_ksum_(i=1)^(n)x_i^(2k)=sum_(i=1)^(n)x_i^ky_i
(8)
or, in matrix form
[n sum_(i=1)^(n)x_i ... sum_(i=1)^(n)x_i^k; sum_(i=1)^(n)x_i sum_(i=1)^(n)x_i^2 ... sum_(i=1)^(n)x_i^(k+1); | | ... |; sum_(i=1)^(n)x_i^k sum_(i=1)^(n)x_i^(k+1) ... sum_(i=1)^(n)x_i^(2k)][a_0; a_1; |; a_k]=[sum_(i=1)^(n)y_i; sum_(i=1)^(n)x_iy_i; |; sum_(i=1)^(n)x_i^ky_i].
(9)
This is a Vandermonde matrix. We can also obtain the matrix for a least squares fit by writing
[1 x_1 ... x_1^k; 1 x_2 ... x_2^k; | | ... |; 1 x_n ... x_n^k][a_0; a_1; |; a_k]=[y_1; y_2; |; y_n].
(10)
Premultiplying both sides by the transpose of the first matrix then gives
[1 1 ... 1; x_1 x_2 ... x_n; | | ... |; x_1^k x_2^k ... x_n^k][1 x_1 ... x_1^k; 1 x_2 ... x_2^k; | | ... |; 1 x_n ... x_n^k][a_0; a_1; |; a_k] =[1 1 ... 1; x_1 x_2 ... x_n; | | ... |; x_1^k x_2^k ... x_n^k][y_1; y_2; |; y_n],
(11)
so
[n sum_(i=1)^(n)x_i ... sum_(i=1)^(n)x_i^k; sum_(i=1)^(n)x_i sum_(i=1)^(n)x_i^2 ... sum_(i=1)^(n)x_i^(k+1); | | ... |; sum_(i=1)^(n)x_i^k sum_(i=1)^(n)x_i^(k+1) ... sum_(i=1)^(n)x_i^(2k)][a_0; a_1; |; a_k]=[sum_(i=1)^(n)y_i; sum_(i=1)^(n)x_iy_i; |; sum_(i=1)^(n)x_i^ky_i].
(12)
As before, given n points (x_i,y_i) and fitting with polynomial coefficients a_0, ..., a_k gives
[y_1; y_2; |; y_n]=[1 x_1 x_1^2 ... x_1^k; 1 x_2 x_2^2 ... x_2^k; | | | ... |; 1 x_n x_n^2 ... x_n^k][a_0; a_1; |; a_k],
(13)
In matrix notation, the equation for a polynomial fit is given by
y=Xa.
(14)
This can be solved by premultiplying by the transpose 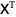X^(T),
X^(T)y=X^(T)Xa.
(15)
This matrix equation can be solved numerically, or can be inverted directly if it is well formed, to yield the solution vector
a=(X^(T)X)^(-1)X^(T)y.
(16)
Setting 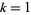k=1 in the above equations reproduces the linear solution.
Posted by at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)